2 - Primeira imagem
2.1 - Visão Geral
Neste capítulo vamos criar a nossa primeira imagem. Em primeiro lugar, e para poder seguir com todo o cuidade este conjunto de passos, aconselhamos a ter disponivel uma vers∆o acutalizada do POV-Ray (versão três) instalada num computador, perto de sí!
Se está a utilizar uma verão com IDE (como por exemplo a do Windows'95) entre no POV-Ray e prepare-se para digitar, passo a passo, os comandos que permitem criar a nossa imagem objectivo! Se está a utilizar uma versão sem IDE, como a de UNIX ou MS-DOS, entre num editor de texto ASCII como o vi ou edit.
2.2 - O sistema de eixos
Para definir-mos um qualquer elemento de um 'programa' POV, temos de saber utilizar o seu sitema de eixos. Este sistema de eixos cartezianos permite especificar precisamente qualquer ponto no universo POV.
Considere-se um sistema coordenado de eixos (tipicamente denominados de x,y e z ou abcissas, ordenadas e cotas).
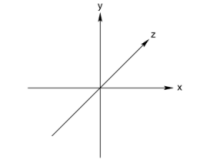
Como se pode verificar no sistema de coordenadas apresentado na imagem anterior, o eixo das abcissas aponta da esquerda para a direita. Portanto, quanto mais um objecto está para a direita, maior é o seu valor das abcissas. Respectivamente, no eixo das coordenadas, quanto mais 'alto' está um objecto, maior é o seu valor de coordenadas. Por ultimo, temos o eixo das cotas. Este, aponta para as tripas do seu monitor. Portanto, quanto maior é a cota de um objecto, mais distante ele está do utilizador.
Note-se que este sistema de eixos é ligeiramente diferente do que estamos habituados quando falamos de geometria (para os que falaram...)!
Para especificar-mos um ponto em POV, usamos a notação <a,b,c> em que a,b e c devem ser substituidos pelos valores respectivos dos eixos das abcissas, ordenadas e cota. Existem ainda três outros vectores (a <a,b,c> chama-se vector!) pre-definidos: são vectores unitários, denominados de x, y e z para definir, respectivamente <1,0,0>, <0,1,0> e <0,0,1>!
Se já compreendeu este sistema de coordenadas, não vai sentir a mínima dificuldade em programar POV! Caso contrário, aconselho a consultar livros mais especificos de geometria!
2.3 - Including
Em POV-Ray podemos utilizar primitivas e conjuntos de objectos definidos em outros ficheiros. Portanto, permite-nos dividir desenhos por ficheiros, por exemplo. Permitiu também, aos criadores do POV-Ray, definir um conjunto de Bibliotecas de cores, formas e texturas.
Qualquer desenho que façamos, deve utilizar bibliotecas, visto que precisariamos de redefinir tudo para as não utilizar. No nosso exemplo, vamos precisar de utilizar algumas: colors.inc, shapes.inc, textures.inc, stones.inc e skies.inc que incluem, respectivamente, definições de cores, formas, texturas, texturas de pedras e padrões para céus.
Para a inclusão de bibliotecas, temos de as ter ou na directoria include da nossa versão de POV-Ray ou então, na directoria onde estamos a trabalhar. Para mais informações sobre directorias, consulte o manual do seu sistema operativo.
No seu programa (até agora vazio...) digite as seguintes linhas de código:
// Os nossos includes...
#include "colors.inc"
#include "shapes.inc"
#include "textures.inc"
#include "stones.inc"
#include "skies.inc" Deve estar agora à voltas a pensar para que serve as duas barras na primeira linha. Essa linha permite escrever um comentário. Um comentário é uma linha de texto que o ajuda a movimentar-se no seu código. Evidentemente que o POV-Ray ignora essa linha, desde as duas barras (//) até ao fim da linha!
Outra forma de incluir coment´rios, de várias linhas, digite o comentário entre /* e */ e será também ignorado.
As cinco linhas seguintes instruem o POV-Ray para que inclua os ficheiros especificados, como se tivessem sido digitados naquele momento no ínicio do nosso texto.
2.4 - Camera
Para definir-mos uma camera temos que especificar a sua localização e o seu alvo. Para tal, utiliza-se o sistema de coordenadas de que falamos no capítulo 2.2. Considere o seguinte exemplo:
camera {
location <.5, .5, -4>
up <0, 1, 0>
right <1.33, 0, 0>
look_at <0, 0, 0>
} Vamos agora analisar o código anterior linha por linha:
A primeira linha diz ao POV-Ray que vamos definir a posição da camera. Note-se que num programa POV só se pode definir uma única! Nas quatro linhas seguintes definimos outros atributos desta camera.
A primitiva location permite definir a posição da camera no universo POV. Neste caso, está a cinco décimas para a direita e para a esquerda do centro do universo, e quatro unidades para fora do monitor ;-). Note-se que o POV-Ray aceita numeros decimais e/ou inteiros positivos e/ou negativos!
As duas linhas seguintes definem o que em inglês é apelidado de aspect ratio. Define a relação entre as unidades dos dois principais eixos (abcissas e ordenadas). Visto que este desenho foi originalmente concebido para colocar no fundo do X-Windows, a sua resolução de compilação foi de 800x600. Se dividir-mos 800 por 600 obtemos um resultado de 1.333333333333333... Portanto, o nosso aspect ratio tem que ser definido de forma a comunicar isso ao POV-Ray, pelo que temos estas duas linhas de código.
Temos ainda uma última linha a explicar: a primitiva look_at. Esta especifica o alvo da camera. Mais uma vez, o parametro que recebe é um vector definido no sistema POV. Neste caso, o nosso alvo é o centro de uma esfera (sshhh... não era para dizer já!) que vamos definir.
2.5 - Uma esfera!
Vamos agora definir o nosso primeiro objecto! Uma esfera. Existe uma primitiva (definida na bilbioteca shapes.inc) que permite definir uma esfera apenas pelo seu centro e raio. Portanto, basta-nos um vector para definir o centro da nossa esfera, um valor real para definir o raio.
O código a aumentar nesta secção é o seguinte:
sphere {
<0, 0, 0>, 1
pigment {
T_Stone1
}
}Depois de ler a primeira linha, o POV-Ray fica a saber que queremos definir uma esfera, pelo que lê de seguida um vector definindo o centro da nossa esfera e o raio da mesma. Queremos a esfera centrada na origem e com raio de uma unidade.
De seguida, temos uma novidade! Vamos aplicar uma textura à nossa esfera! Dentro do primitiva sphere, definimos uma textura com a primitiva pigment (que pode ser utilizada com todas as primitivas). T_Stone1 é uma definição de uma textura pré-definida na biblioteca stones.inc.
Para saber todas as texturas definidas numa biblioteca, consulte alguns ficheiros de texto na mesma directoria onde estão as texturas, ou as próprias texturas.
Falaremos de novo em texturas, mais para a frente!
2.6 - Agora temos um Plano!
Não... não é um plano de assalto! Vamos criar um plano para que a nossa esfera não fique a flutuar no nosso universo! Para tal, utilizamos a primitiva plane. Temos como parametros, um vector e um real.
O vector aponta na direcção normal ao plano e para o lado exterior do plano (lado onde a textura vai ser aplicada). Este vector faz um ângulo de 90 graus em relação ao plano a criar!
O real que definimos de seguida é a distância entre o plano e a origem no seu vector normal! Considere o código do nosso plano:
plane {
<0, 1, 0>, -1
pigment {
White_Marble
}
rotate <0, 45, 0>
} Depois de ler este código deve ter tido dificuldade apenas na primitiva rotate. Esta primitiva permite fazer uma rotação a um objecto em relação a um dos três eixos. No nosso caso estamos a dar uma rotação à volta do eixo das ordenadas para que a textura (White_Marble) fique numa posição mais bonita. Como vemos, esta primitiva não tem nada que saber. É necessário pelo menos alguma prática para o utilizar decentemente!
2.7 - Céu
Uma coisa que nos faz falta além de um plano onde pousar a esfera e a própria esfera, é o céu ou o tecto do nosso universo! No caso da imagem que estamos a tentar criar, queria um céu!
Exite, a partir da versão três do POV-Ray uma primitiva denominada sky_sphere que faz isso mesmo: cria um céu transparente à luz e à sombra. Para definir um céu basta-nos especificar uma textura! Esta textura é normalmente uma das da biblioteca skies.inc uma vez que define quase todos os céus de que alguma vez precisaremos (pelo menos para já!).
O código referente ao nosso céu é:
sky_sphere {
S_Cloud1
} 2.8 - Luz..
Para a definição simples de uma fonte de luz, basta-nos um ponto, e uma cor! Uma cor sim! A luz tem cor. Podemos defini-las verdes, amarelas, pretas (não iluminam :-)), brancas, etc, etc...
A primitiva usada é light_source seguida de um vector especificando a localização da fonte de luz e a sua cor!
Para o nosso desenho, temos como exemplo:
light_source {
<-9, 1, -9> color White}
light_source {
<0, 0, 4> color Blue}
light_source {
<2, 0, 5> color Red}
light_source {
<-2, 5, 8> color Green} Para definir-mos uma cor, podemos utilizar uma declarada numa biblioteca (neste exemplo, na colors.inc) ou então, definir-mos a nossa cor. Para isso utiliza-se a primitiva color da seguinte forma:
color red 1 green .6 blue 1 Em que os valores numéricos indicam a quantidade dessa cor a misturar. Os valores devem estar compreendidos entre 0 e 1, respectivamente, sendo o 0 o não existir essa cor e o 1, o máximo dessa cor!
2.9 - Compilar
Se utiliza a versão para Windows'95, basta premir um botão para compilar o seu desenho! Prima as teclas Ctrl + G (G=Go!) e aparecerá uma janela com a sua imagem, enquanto que o POV a vai compilando!
Se utiliza uma versão sem IDE, tem um pouco mais de trabalho! Em primeiro lugar vai ter de chamar o POV-Ray pela linha de comando de modo a compilar o seu desenho e depois utilizar um programa de tratamento gráfico para ver a imagem!
Vamos apenas explicar a primeira metade do parágrafo anterior. Execute o seguinte comando:
povray +Iname.pov +Oname.tga
+V +W320 +H240Em que deve substituir name.pov pelo nome do ficheiro com que gravou o código, e name.tga pelo nome do ficheiro tga que quer obter! O +V indica ao POV-Ray para ir dando informações acerca da compilação! O +W e o +H especificam, respectivamente, a largura e a altura da imagem! Note que para o desenho que fizemos convem que a largura a dividir pela largura seja igual a 1.333333!
2.10 - O resultado!!
